题目内容
2.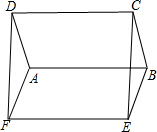 如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.
如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.
分析 由平行四边形的性质得出AB∥CD,AB=CD,AB∥EF,AB=EF,因此CD∥EF,CD=EF,证出四边形EFDC是平行四边形,再由等腰三角形的三线合一性质得出AB⊥CE,因此CD⊥CE,得出∠DCE=90°,即可得出结论.
解答 证明:∵在?ABCD与?ABEF中,AB∥CD,AB=CD,AB∥EF,AB=EF,
∴CD∥EF,CD=EF,
∴四边形EFDC是平行四边形,
∵BC=BE,∠ABC=∠ABE,
∴AB⊥CE,
∴CD⊥CE,
∴∠DCE=90°,
∴四边形EFDC是矩形.
点评 本题考查了平行四边形的判定与性质、矩形的判定、等腰三角形的三线合一性质;熟练掌握平行四边形的判定与性质,由等腰三角形的三线合一性质证出CD⊥CE是解决问题的关键.

练习册系列答案
相关题目
13.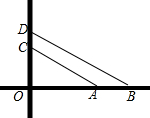 如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
 如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )| A. | 5m | B. | 4m | C. | 3m | D. | 2m |
10.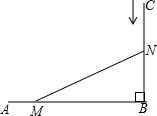 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
15.我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
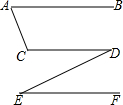 如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.
如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF. 如图,已知BE∥AO,∠1=∠2,OE⊥OA于点O,求证:∠4+∠5=90°.
如图,已知BE∥AO,∠1=∠2,OE⊥OA于点O,求证:∠4+∠5=90°.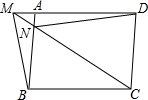 如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.
如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.