题目内容
1.估计$2\sqrt{6}-1$的值在( )| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
分析 由于2$\sqrt{6}$=$\sqrt{24}$,先利用逼近法估算$\sqrt{24}$在哪两个连续的整数之间,再根据不等式的性质即可求解.
解答 解:2$\sqrt{6}$=$\sqrt{24}$,
∵16<24<25,
∴4<$\sqrt{24}$<5,
∴4-1<$\sqrt{24}$-1<5-1,
即3<$\sqrt{24}$-1<4.
故选B.
点评 本题考查了估算无理数的大小,不等式的性质,正确估算出$\sqrt{24}$在哪两个连续的整数之间是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
9. 如图,已知AB∥CD,则∠α=( )
如图,已知AB∥CD,则∠α=( )
 如图,已知AB∥CD,则∠α=( )
如图,已知AB∥CD,则∠α=( )| A. | 85° | B. | 60° | C. | 75° | D. | 80° |
16.下列命题是假命题的是( )
| A. | 等角的补角相等 | B. | 内错角相等 | ||
| C. | 两点之间,线段最短 | D. | 同旁内角互补,两直线平行 |
13.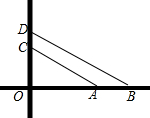 如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
 如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )
如图表示的是一个十字路口,O是两条公路的交点,点A、B、C、D表示的是公路上的四辆车,若OC=8cm,AC=17cm,AB=5cm,BD=10$\sqrt{5}$m,则C,D两辆车之间的距离为( )| A. | 5m | B. | 4m | C. | 3m | D. | 2m |
10.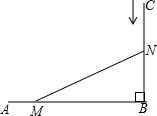 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.




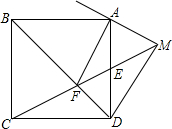 如图,边长为4的正方形ABCD中,E为AD的中点,连接CE交BD于F,连接AF,过A作AM⊥AF交CE的延长线于M,则DM的长为$\sqrt{13}$.
如图,边长为4的正方形ABCD中,E为AD的中点,连接CE交BD于F,连接AF,过A作AM⊥AF交CE的延长线于M,则DM的长为$\sqrt{13}$.