题目内容
3.计算:($\sqrt{24}$-$\sqrt{2}$)-($\sqrt{8}$+$\sqrt{6}$)分析 先把二次根式化为最简二次根式,再去括号,然后合并同类二次根式,即可得出答案.
解答 解:($\sqrt{24}$-$\sqrt{2}$)-($\sqrt{8}$+$\sqrt{6}$)
=2$\sqrt{6}$-$\sqrt{2}$-2$\sqrt{2}$-$\sqrt{6}$
=$\sqrt{6}$-3$\sqrt{2}$.
点评 此题考查了二次根式的化简求值,在计算时要注意运算顺序和结果的符号,把二次根式化成最简再计算.

练习册系列答案
相关题目
10.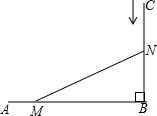 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
8.某个正数的两个平方根分别是a-1和3-2a,则实数a的值为( )
| A. | 4 | B. | -$\frac{4}{3}$ | C. | 2 | D. | -2 |
15.我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
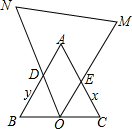 如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.
如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.