题目内容
19.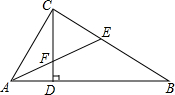 如图所示,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,求证:CF=CE.
如图所示,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,求证:CF=CE.
分析 根据直角三角形的性质和角平分线的定义证明即可.
解答 证明:∵∠ACB=90°,
∴∠CAE+∠CEF=90°,
∵CD是AB边上的高,
∴∠FAD+∠AFD=90°,
∵AE是∠CAB的平分线,
∴∠CAE=∠FAD,
∴∠CEF=∠AFD,又∵∠AFD=∠CFE,
∴∠CFE=∠CEF,
∴CF=CE.
点评 本题考查的是直角三角形的性质,等腰三角形的判定和性质,直角三角形的两锐角互余是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
9. 如图,已知AB∥CD,则∠α=( )
如图,已知AB∥CD,则∠α=( )
 如图,已知AB∥CD,则∠α=( )
如图,已知AB∥CD,则∠α=( )| A. | 85° | B. | 60° | C. | 75° | D. | 80° |
10.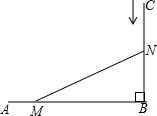 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
4.给出下列命题:①一组对边和一组对角分别相等的四边形是平行四边形;②两组对角的内角平分线分别平行的四边形是平行四边形;③一组对边中点间的距离等于另一组对边长和的一半的四边形是平行四边形;④两条对角线都平分四边形的面积的四边形是平行四边形.其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下表列出了一项试验统计数据,表示将皮球从高处落下时,下落高度d与弹跳高度b的关系:
(1)下落高度d与弹跳高度b之间的函数解析式是C
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
A.b=d2 B.b=2d C.b=$\frac{d}{2}$ D.b=d+25
(2)求当d=10时的弹跳高度b;
(3)求当弹跳高度b是100时的下落高度d.
8.某个正数的两个平方根分别是a-1和3-2a,则实数a的值为( )
| A. | 4 | B. | -$\frac{4}{3}$ | C. | 2 | D. | -2 |
 如图,已知BE∥AO,∠1=∠2,OE⊥OA于点O,求证:∠4+∠5=90°.
如图,已知BE∥AO,∠1=∠2,OE⊥OA于点O,求证:∠4+∠5=90°.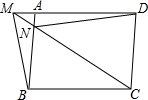 如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.
如图,已知:?ABCD,M是DA延长线上一点,连接MB,MC,且MC交AB于点N,连接DN,求证:S△BMN=S△AND.