题目内容
1.解方程组:(1)$\left\{\begin{array}{l}{3s+t=5}\\{s+2t=15}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+2y+3z=11}\\{x-y+4z=10}\\{x+3y+2z=2}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法变形为二元一次方程组,再利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3s+t=5①}\\{s+2t=15②}\end{array}\right.$,
①×2-②得:5s=-5,即s=-1,
把s=-1代入①得:t=8,
则方程组的解为$\left\{\begin{array}{l}{s=-1}\\{t=8}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+2y+3z=11①}\\{x-y+4z=10②}\\{x+3y+2z=2③}\end{array}\right.$,
①+②×2得:3x+11z=31④,
②×3+③得:2x+7z=16⑤,
④×2-⑤×3得:z=14,
把z=14代入⑤得:x=-41,
把x=-41,z=14代入②得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=-41}\\{y=5}\\{z=14}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
11.甲工程队完成1000米的施工任务,乙甲工程队完成1200米的施工任务,两队同时开工且恰好同时完工,甲队比乙队每天少做20米.设乙队每天施工x米,根据题意,下面所列方程正确的是( )
| A. | $\frac{1000}{x}$=$\frac{1200}{x-20}$ | B. | $\frac{1000}{x-20}$=$\frac{1200}{x}$ | C. | $\frac{1000}{x}$=$\frac{1200}{x+20}$ | D. | $\frac{1000}{x+20}$=$\frac{1200}{x}$ |
12.若a>b,则下列不等式变形正确的是( )
| A. | a-3<b-3 | B. | $\frac{a}{5}$<$\frac{b}{5}$ | C. | -3a>-3b | D. | 3-2a<3-2b |
10.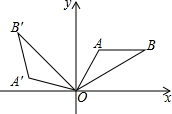 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
 如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )
如图,将△OAB绕原点0逆时针旋转105°到△OA′B′的位置,若AB∥x轴,OA=AB,OB=2,∠A=120°,则点B′的坐标为( )| A. | (-2,2$\sqrt{2}$) | B. | (-2$\sqrt{2}$,2) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
 按要求画出图形:
按要求画出图形: 已知,∠α
已知,∠α 在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.
在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.