题目内容
9. 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.
分析 当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经是一条线段,只需考虑始点和终点位置即可解决问题.当m=$\frac{1}{3}$时,连接PM,如图1,点M从点A绕着点P逆时针旋转了一周的$\frac{1}{3}$,从而可得到旋转角为120°,则∠APM=120°,根据PA=PM可得∠PAM=30°,在Rt△AON中运用三角函数可求出ON的长;当m=$\frac{2}{3}$时,连接PM,如图2,点M从点A绕着点P逆时针旋转了一周的$\frac{2}{3}$,从而可得到旋转角为240°,则∠APM=120°,同理可求出ON的长,问题得以解决.
解答 解:①当m=$\frac{1}{3}$时,连接PM,如图1,
∠APM=$\frac{1}{3}$×360°=120°.
∵PA=PM,∴∠PAM=∠PMA=30°.
在Rt△AON中,NO=AO•tan∠OAN=1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$.
②当m=$\frac{2}{3}$时,连接PM,如图2,
∠APM=360°-$\frac{2}{3}$×360°=120°,
同理可得:NO=$\frac{\sqrt{3}}{3}$.
综合①、②可得:点N相应移动的路经长为$\frac{\sqrt{3}}{3}$+$\frac{\sqrt{3}}{3}$=$\frac{2}{3}\sqrt{3}$.
故答案为$\frac{2}{3}$$\sqrt{3}$.
点评 本题主要考查了旋转角、等腰三角形的性质、三角函数等知识,若动点的运动路径是一条线段,常常可通过考虑临界位置(动点的始点和终点)来解决.

练习册系列答案
相关题目
19.下列运算中,正确的是( )
| A. | x+x2=x3 | B. | 2x3÷x2=x | C. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{8}$ | D. | (a+4)(a+3)=a2+12 |
14.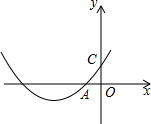 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
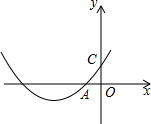 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )| A. | ac+1=b | B. | ab+1=c | C. | bc+1=a | D. | 以上都不是 |
18. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
 在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).
在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).
 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).