题目内容
14.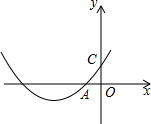 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )| A. | ac+1=b | B. | ab+1=c | C. | bc+1=a | D. | 以上都不是 |
分析 根据图象易得C(0,c)且c>0,再利用OA=OC可得A(-c,0),然后把A(-c,0)代入y=ax2+bx+c即可得到a、b、c的关系式.
解答 解:当x=0时,y=ax2+bx+c=c,则C(0,c)(c>0),
∵OA=OC,
∴A(-c,0),
∴a•(-c)2+b•(-c)+c=0,
∴ac-b+1=0,
即ac+1=b.
故选A.
点评 本题考查了二次项系数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
5.下列计算正确的是( )
| A. | a3+a2=2a5 | B. | (2ab2)3=6a3b6 | ||
| C. | 2a2b•3ab2=6a2b3 | D. | x3y2÷(-2x2y)=-$\frac{1}{2}$xy |
3.已知点A(-2,y1),B(3,y2)是反比例函数y=$\frac{k}{x}$(k<0)图象上的两点,则有( )
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
4.陆地上最高处是珠穆朗玛峰顶,高出海平面8844m,记为+8844m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为( )
| A. | +415m | B. | -415m | C. | ±415m | D. | -8848m |

 如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$.
如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$. 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1,点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0).设点M转过的路程为m(0<m<1),随着点M的转动,当m从$\frac{1}{3}$变化到$\frac{2}{3}$时,点N相应移动的路经长为$\frac{2}{3}\sqrt{3}$.
