题目内容
12.写出下列抛物线的开口方向、对称轴和顶点.(1)y=3(x-2)2+1;
(2)y=-$\frac{2}{3}$(x+1)2-5;
(3)y=2(x-3)2-$\frac{1}{3}$;
(4)y=-$\frac{1}{5}$(x+5)2+2.
分析 已知抛物线解析式都是顶点式,可根据顶点式的坐标特点求开口方向,顶点坐标及对称轴.
解答 解:(1)y=3(x-2)2+1,开口向上,对称轴是直线x=2,顶点坐标为(2,1);
(2)y=-$\frac{2}{3}$(x+1)2-5,开口向下,对称轴是直线x=-1,顶点坐标为(-1,-5);
(3)y=2(x-3)2-$\frac{1}{3}$,开口向上,对称轴是直线x=3,顶点坐标为(3,-$\frac{1}{3}$);
(4)y=-$\frac{1}{5}$(x+5)2+2,开口向下,对称轴是直线x=-5,顶点坐标为(-5,2).
点评 此题考查二次函数的性质,根据抛物线的顶点式,可确定抛物线的开口方向,顶点坐标(对称轴),最大(最小)值,增减性等.

练习册系列答案
相关题目
 如图,AB∥CD,AD与BC交于O点,AO=4,OB=6,AD=16,求BC、OC.
如图,AB∥CD,AD与BC交于O点,AO=4,OB=6,AD=16,求BC、OC. 如图所示,扇形纸扇完全打开后,$\widehat{BC}$的长度为20π,$\widehat{DE}$的长度为$\frac{40}{3}$π,AB=30,BD=20,求∠BAC的度数以及贴纸部分(阴影部分)的面积.
如图所示,扇形纸扇完全打开后,$\widehat{BC}$的长度为20π,$\widehat{DE}$的长度为$\frac{40}{3}$π,AB=30,BD=20,求∠BAC的度数以及贴纸部分(阴影部分)的面积.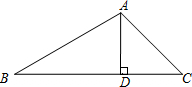 如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积.
如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积.