题目内容
14．
如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数．
分析 如图所示，由三角形外角的性质可知：∠A+∠B=∠IJL，∠C+∠D=∠MLJ，∠H+∠K=∠GIJ，∠E+∠F=∠GML，然后由多边形的内角和公式可求得答案．
解答 解：如图所示：
由三角形的外角的性质可知：∠A+∠B=∠IJL，∠C+∠D=∠MLJ，∠H+∠K=∠GIJ，∠E+∠F=∠GML，
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=∠IJL+∠MLJ+∠GML+∠G+∠GIJ=（5-2）×180°=3×180°=540°．
点评 本题主要考查的是三角形外角的性质和多边形的内角和公式的应用，利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键．
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12．
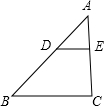如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AE=3，EC=6，则$\frac{AD}{AB}$的值为（ ）
如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AE=3，EC=6，则$\frac{AD}{AB}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
13．下列说法中正确的是（ ）
| A． | 平分弦的直径垂直于弦 | |
| B． | 圆心角是圆周角的2倍 | |
| C． | 三角形的外心到三角形各边的距离相等 | |
| D． | 从圆外一点可以引圆的两条切线，这一点和圆心的连线平分两条切线的夹角 |
如图，将一副三角板叠放在一起，使直角的顶点重合于点O，则∠AOD+∠COB的度数为180度．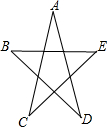
如图，则∠A+∠B+∠C+∠D+∠E的度数是180°．
如图，求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数．
如图，已知DC是∠ACB的外角平分线，∠BAC与∠1的大小关系如何？∠BAC与∠2呢？∠2与∠B呢？∠BAC与∠B呢？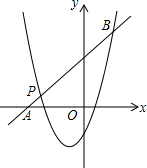
已知二次函数y1=x2+mx+n的图象经过点P（-3，1），对称轴是经过（-1，0）且平行于y轴的直线．