题目内容
19. 如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
分析 首先根据三角形的外角的性质和四边形的内角和即可得到结论.
解答  解:如图,
解:如图,
∵∠10=∠4+∠9,∠11=∠4+∠8,
∴∠10+∠11=∠4+∠9+∠4+∠8=180°+∠4,
∴(∠2+∠3+∠1+∠11)+(∠5+∠6+∠7+∠10)
=360°+360°
=720°
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=720°-180°=540°,
即∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数是540°.
点评 (1)此题主要考查了多边形的内角和外角的性质和应用,要熟练掌握.
(2)此题还考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.

练习册系列答案
相关题目
18. 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )| A. | AD=$\frac{1}{2}$CD | B. | AC=$\frac{1}{2}$AB | C. | BD=$\frac{1}{2}$BC | D. | CD=$\frac{1}{2}$AB |
11. 已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
 已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )| A. | 70° | B. | 85° | C. | 65° | D. | 以上都不对 |

 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数.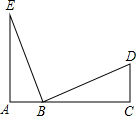 如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.