题目内容
已知(x2＋px＋8)(x2－3x＋q)的展开式中不含x2和x3项，求p，q的值．
p＝3，q＝1.
【解析】试题分析：根据整式的乘法，化简完成后，根据不含项的系数为0求解即可.
试题解析：∵（x2+px+8）（x2﹣3x+q）
=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q
=x4+（p﹣3）x3+（q﹣3p+8）x2+（pq﹣24）x+8q．
∵乘积中不含x2与x3项，
∴p﹣3=0，q﹣3p+8=0，
∴p=...
练习册系列答案
相关题目
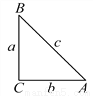
如图，在Rt△ABC中，BC、AC、AB三边的长分别为a、b、c，则sinA＝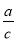
，cosA＝
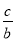，tanA＝
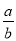.我们不难发现：sin260°＋cos260°＝1，…，试探求sinA、cosA、tanA之间存在的一般关系，并说明理由．
sin2A＋cos2A＝1，tanA＝，理由见解析.
【解析】试题分析：sin2A＋cos2A＝1，tanA＝，根据三角函数的定义以及勾股定理通过推导即可得.
试题解析：sin2A＋cos2A＝1，tanA＝，理由如下：
∵∠C=90°，∴a2+b2=c2，sinA＝，cosA＝，tanA＝，
∴sin2A+cos2A＝；
tanA＝.. 下列语句错误的是( )
A. 锐角的补角一定是钝角 B. 一个锐角和一个钝角一定互补
C. 互补的两角不能都是钝角 D. 互余且相等的两角都是45°
B
【解析】A. ∵锐角小于90°，∴ 锐角的补角一定是钝角，故正确；
B. ∵如：30°+100°=130°，∴一个锐角和一个钝角不一定互补，故不正确；
C. ∵如果两个角都是钝角，则其和就大于180°，∴互补的两角不能都是钝角，故正确；
D. ∵互余且相等的两角都是45°，故正确；
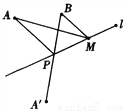
故选B. 已知：如图，A、B两点在直线l的同侧，点A'与A关于直线l对称，连接A'B交l于P点，若A'B＝a.
（1）求AP＋PB；
（2）若点M是直线l上异于P点的任意一点，求证：AM＋MB＞AP＋PB．
答案见解析
【解析】试题分析： 由轴对称的性质可知： 从而可求得答案；
由两点之间线段最短进行证明即可．
试题解析：(1)∵点A′与A关于直线l对称，
∴PA=PA′.
∴PA+PB=PA′+PB=A′B=a.
(2)∵点A′与A关于直线l对称，
∴MA=MA′.
∴AM+BM=MA′+MB.
由(1)可知：AP+PB=A′B
由两点之间线段... 如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是（ ）．
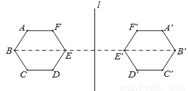
A．AB=A′B′ B．BC∥B′C′ C．直线l⊥BB′ D．∠A′=120°
B．
【解析】
试题分析：关于轴对称的两个图形沿对称轴翻折，能够重合，两个图形是全等形，对应边相等，所以A正确；C正确，因为正六边形的一个内角是120度，所以D正确．故本题选B． 已知a+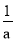
=5,则a2+
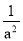的结果是___________.
23
【解析】由题意知=25,即a2++2=25,所以a2+=23. 已知27m-1÷32m=27,则m=___________.
6
【解析】由题意知，(33)m-1÷32m=27.
所以33(m-1)-2m=33.
所以3m-3-2m=3，解得m=6. 如图，从镜子中看到一钟表的时针和分针，此时的实际时刻是________.
9:30
【解析】【解析】
生活中的镜面对称，在数学当中为轴对称，根据这个原理，很容易得到此时的实际时刻是9：30．故答案为：9：30． 某水果店卖出的香蕉数量（千克）与售价（元）之间的关系如表：
数量（千克） | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
售价（元） | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | … |
上表反映了________个变量之间的关系，其中，自变量是________；因变量是________．
两 香蕉数量 售价
【解析】∵香蕉的售价随着香蕉数量的变化而变化
∴上表反映了两个变量之间的关系，其中，自变量是香蕉数量；因变量是售价.