题目内容
3.把下列各式分解因式;(1)xy3+x4;
(2)x4-xy3;
(3)a2(m+n)3-a2b3;
(4)y2(x2-2x)3+y2.
分析 (1)先提取公因式x,再利用立方和公式分解;
(2)先提取公因式x,再利用立方差公式分解;
(3)先提取公因式a2,再利用立方差公式分解;
(4)先提取公因式y2,再利用立方和公式分解;
解答 解:(1)原式=x(y3+x3)=x(y+x)(y2-xy+x2);
(2)原式=x(x3-y3)=x(x-y)(x2+xy+y2);
(3)原式=a2(m+n-b)(m2+2mn+n2+bm+bn+b2);
(4)原式=y2(x2-2x+1)[(x2-2x)2-(x2-2x)+1]=y2(x-1)2(x4-4x3+3x2+1).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.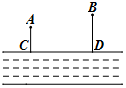 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )| A. | 距C点1km处 | B. | 距C点2km处 | C. | 距C点3km处 | D. | CD的中点处 |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( ) 如图,在四边形ABCD中,已知AB=3,BC=12,CD=13,DA=4,且∠DAB=90°,求这个四边形的面积.
如图,在四边形ABCD中,已知AB=3,BC=12,CD=13,DA=4,且∠DAB=90°,求这个四边形的面积.