题目内容
17. 如图,在四边形ABCD中,已知AB=3,BC=12,CD=13,DA=4,且∠DAB=90°,求这个四边形的面积.
如图,在四边形ABCD中,已知AB=3,BC=12,CD=13,DA=4,且∠DAB=90°,求这个四边形的面积.
分析 根据题意作出合适的辅助线,然后根据勾股定理可以求得BD的长,然后根据勾股定理的逆定理可以判断△BDC的形状,从而可以解答本题.
解答  解:连接BD,
解:连接BD,
∵在△ABD中,∠DAB=90°,
∴BD2=AB2+AD2=32+42=25,
∴BD=5,
∵在△DBC中,DB2+BC2=52+122=25+144=169,CD2=132=169,
∴DB2+BC2=CD2,
∴△DBC是直角三角形,
∴∠DBC=90°,
∴S四边形ABCD=S△DAB+S△DBC=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=36.
点评 本题考查勾股定理、勾股定理的逆定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
2.对二次三项式x2-4x-1变形正确的是( )
| A. | (x+2)2-5 | B. | (x+2)2+3 | C. | (x-2)2-5 | D. | (x-2)2+3 |
12.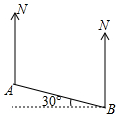 A、B两地的位置如图所示,则A在B的( )
A、B两地的位置如图所示,则A在B的( )
 A、B两地的位置如图所示,则A在B的( )
A、B两地的位置如图所示,则A在B的( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
9.如果关于x的不等式(a+5)x>a+5的解集为x<1那么,a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-5 | D. | a<-5 |
6.我市4月份某天的最高气温是22℃,最低气温是8℃,那么这天的温差是( )
| A. | 30℃ | B. | 14℃ | C. | -14℃ | D. | 12℃ |
7.在不等式$\frac{2}{3}$x+2>x的解集中,正整数解的个数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
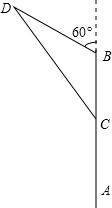 如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.
如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.