题目内容
15.(1)$\frac{x\sqrt{y}-y\sqrt{x}}{x\sqrt{y}+y\sqrt{x}}-\frac{y\sqrt{x}+x\sqrt{y}}{y\sqrt{x}-x\sqrt{y}}$;(2)$\frac{2}{b}\sqrt{a{b}^{5}}.(-\frac{3}{2}\sqrt{{a}^{3}b})÷3\sqrt{\frac{b}{a}}$.
分析 (1)先将两式分子、分母都提取$\sqrt{xy}$、约分,再通分化为同分母的代数式相减,计算可得;
(2)根据二次根式的混合运算顺序计算可得.
解答 解:(1)原式=$\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}(\sqrt{x}+\sqrt{y})}$-$\frac{\sqrt{xy}(\sqrt{y}+\sqrt{x})}{\sqrt{xy}(\sqrt{y}-\sqrt{x})}$
=$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$-$\frac{\sqrt{y}+\sqrt{x}}{\sqrt{y}-\sqrt{x}}$
=$\frac{(\sqrt{x}-\sqrt{y})(\sqrt{y}-\sqrt{x})}{(\sqrt{y}+\sqrt{x})(\sqrt{y}-\sqrt{x})}$-$\frac{(\sqrt{y}+\sqrt{x})(\sqrt{y}+\sqrt{x})}{(\sqrt{y}-\sqrt{x})(\sqrt{y}+\sqrt{x})}$
=$\frac{\sqrt{xy}-x-y+\sqrt{xy}-(x+y+2\sqrt{xy})}{y-x}$
=$\frac{-2x-2y}{y-x}$
=$\frac{2x+2y}{x-y}$;
(2)原式=(-$\frac{2}{b}$×$\frac{3}{2}$×$\frac{1}{3}$)•$\sqrt{a{b}^{5}•{a}^{3}b•\frac{a}{b}}$
=-$\frac{1}{b}$•$\sqrt{{a}^{5}{b}^{5}}$
=-$\frac{1}{b}$•a2b2$•\sqrt{ab}$
=-a2b$\sqrt{ab}$.
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

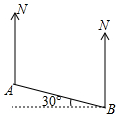 A、B两地的位置如图所示,则A在B的( )
A、B两地的位置如图所示,则A在B的( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
| A. | a>0 | B. | a<0 | C. | a>-5 | D. | a<-5 |
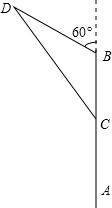 如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.
如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.