题目内容
12.解方程组:$\left\{\begin{array}{l}{x+y-z=6}\\{x-3y+2z=1}\\{3x+2y-z=4}\end{array}\right.$.分析 ①-③得出2x+y=-2④,②+③×2得出7x+y=9⑤,由④和⑤组成一个二元一次方程组,求出x、y的值,把x、y的值代入①求出z即可.
解答 解:$\left\{\begin{array}{l}{x+y-z=6①}\\{x-3y+2z=1②}\\{3x+2y-z=4③}\end{array}\right.$
①-③得:-2x-y=2,
即2x+y=-2④,
②+③×2得:7x+y=9⑤,
由④和⑤组成一个二元一次方程组$\left\{\begin{array}{l}{2x+y=-2}\\{7x+y=9}\end{array}\right.$,
解得:x=$\frac{11}{5}$,y=-$\frac{32}{5}$,
把x、y的值代入①得:$\frac{11}{5}$-$\frac{32}{5}$-z=6,
解得:z=-$\frac{51}{5}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{11}{5}}\\{y=-\frac{32}{5}}\\{z=-\frac{51}{5}}\end{array}\right.$.
点评 本题考查了解三元一次方程组的应用,解此题的关键是能把三元一次方程组转化成二元一次方程组,难度适中.

练习册系列答案
相关题目
7. 如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
 如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
4.下列方程组是三元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{3x+5y+z=-8}\\{x+y+m=3}\\{x-2y+z=21}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=2}\\{z=3}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3}\\{y+z=-1}\\{z+w=8}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a+b=9}\\{2d-ab=2}\\{a-b+d=0}\end{array}\right.$ |
 如图,点B、E、C、F在同一条直线上,BE=CF,AB∥DF,AB=DF.试判断四边形AEDC的形状,并说明理由.
如图,点B、E、C、F在同一条直线上,BE=CF,AB∥DF,AB=DF.试判断四边形AEDC的形状,并说明理由.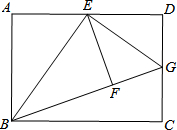 如图,矩形ABCD中,AD>AB,AB=1,点E是AD的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,连结EG.
如图,矩形ABCD中,AD>AB,AB=1,点E是AD的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,连结EG.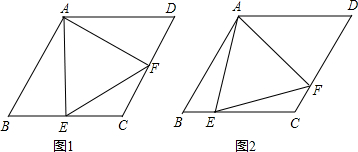
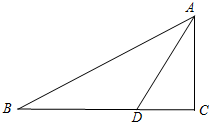 已知在Rt△ABC中,AC⊥BC,AD是∠BAC的角分线,以AB上的一点O为圆心,AD为弦作⊙O.
已知在Rt△ABC中,AC⊥BC,AD是∠BAC的角分线,以AB上的一点O为圆心,AD为弦作⊙O.