题目内容
7. 如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图,Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$(k≠0)经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
分析 设OA=a,AE=b,则C点坐标(-a,-$\frac{k}{a}$),B点坐标(-a-b,-$\frac{k}{a}$),根据S△BCD=2S△ACD=6得出S△ACB=9=$\frac{1}{2}$AC•BC=$\frac{1}{2}$•(-$\frac{k}{a}$)•b得出bk=-18a①,先求得D的坐标,根据点D在双曲线上,得出(-$\frac{1}{3}$b-a)•(-$\frac{1}{3}$•$\frac{k}{a}$)=k,则b=6a②,结合①②,即可求得k的值.
解答 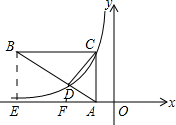 解:设OA=a,AE=b,则C点坐标(-a,-$\frac{k}{a}$),B点坐标(-a-b,-$\frac{k}{a}$)
解:设OA=a,AE=b,则C点坐标(-a,-$\frac{k}{a}$),B点坐标(-a-b,-$\frac{k}{a}$)
∵BD=2AD,
∴S△BCD=2S△ACD=6,
∴S△ACB=9=$\frac{1}{2}$AC•BC=$\frac{1}{2}$•(-$\frac{k}{a}$)•b得bk=-18a,
∵B点坐标(-a-b,-$\frac{k}{a}$),BD=2AD,
∴D点坐标(-$\frac{1}{3}$b-a,-$\frac{1}{3}$•$\frac{k}{a}$),
∵点D在双曲线上,
则(-$\frac{1}{3}$b-a)•(-$\frac{1}{3}$•$\frac{k}{a}$)=k,
则b=6a,
解$\left\{\begin{array}{l}{bk=-18a}\\{b=6a}\end{array}\right.$得k=-3.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,求得D点的坐标是本题的关键.

练习册系列答案
相关题目
2.将二次函数y=x2的图象如何平移可得到y=x2-2x+2的图象( )
| A. | 向左平移2个单位,向上平移2个单位 | |
| B. | 向右平移2个单位,向下平移2个单位 | |
| C. | 向右平移1个单位,向上平移1个单位 | |
| D. | 向左平移1个单位,向下平移1个单位 |
17.2014年成都市的国民生产总值为1034亿元,1034亿元用科学记数法表示正确的是( )
| A. | 1034×108元 | B. | 1.034×1011元 | C. | 1.0×1011元 | D. | 1.034×1012元 |
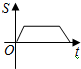
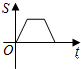
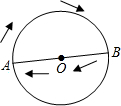 如图,小虎在篮球场上玩,从点O出发,沿着O→A→B→O的路径匀速跑动,能近似刻画小虎所在位置距出发点O的距离S与时间t之间的函数关系的大致图象是( )
如图,小虎在篮球场上玩,从点O出发,沿着O→A→B→O的路径匀速跑动,能近似刻画小虎所在位置距出发点O的距离S与时间t之间的函数关系的大致图象是( )