题目内容
3.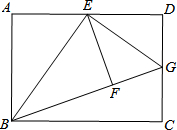 如图,矩形ABCD中,AD>AB,AB=1,点E是AD的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,连结EG.
如图,矩形ABCD中,AD>AB,AB=1,点E是AD的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,连结EG.(1)求证:△EFG≌△EDG;
(2)若点G恰是CD边的中点,求AD的长;
(3)若△ABE与△BCG相似,求AD的长.
分析 (1)由△FBE是由△ABE翻折得到的,利用HL,即可求得Rt△EFG≌Rt△EDG,则可证得DG=FG;
(2)由G是CD的中点,得到DG与CG的值,在Rt△BCG中,利用勾股定理即可求得AD的长;
(3)由平行线与翻折变换的性质,易得:∠ABE=$\frac{1}{2}$∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
解答 (1)证明:∵△FBE是由△ABE翻折得到的,
∴AE=FE,∠EFB=∠EAB=90°,
∴∠EFG=∠EDG=90°.
∵AE=DE,
∴FE=DE.
∴在Rt△EFG与Rt△EDG中,
$\left\{\begin{array}{l}{EF=ED}\\{EG=EG}\end{array}\right.$,
∴Rt△EFG≌Rt△EDG(HL).
∴DG=FG;
(2)解:若G是CD的中点,则DG=CG=$\frac{1}{2}$,
∵在Rt△BCG中,BC=$\sqrt{B{G}^{2}-C{G}^{2}}$=$\sqrt{2}$,
∴AD=$\sqrt{2}$.
(3)解:由题意AB∥CD,
∴∠ABG=∠CGB.
∵△FBE是由△ABE翻折得到的,
∴∠ABE=∠FBE=$\frac{1}{2}$∠ABG,
∴∠ABE=$\frac{1}{2}$∠CGB.
∴若△ABE与△BCG相似,则必有∠ABE=∠CBG=30°.
在Rt△ABE中,AE=ABtan∠ABE=$\frac{\sqrt{3}}{3}$,
∴AD=2AE=$\frac{2\sqrt{3}}{3}$.
点评 此题考查了翻折变换的性质,相似三角形的性质,全等三角形的判定与性质以及勾股定理等知识.此题综合性很强,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
10.某学校绿化小组,在植树节这天种下银杏树的棵数如下:10,6,11,8,10,9,则这组数据中的中位数是( )
| A. | 8 | B. | 9 | C. | 9.5 | D. | 10 |
7.如果相切两圆的半径分别为3和1,那么它们的圆心距是( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | 无法确定 |
13.中国的陆地面积约为9600000km.将9600000用科学记数法表示应为( )
| A. | 96×106 | B. | 96×105 | C. | 9.6×107 | D. | 9.6×106 |
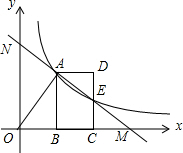 如图,反比例函数k=xy(x>0)的图象经过线段OA的端点A,O为原点,作AB垂直于x轴于点B,点B的坐标为(2,0),tan∠AOB=2.
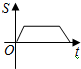
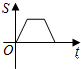
如图,反比例函数k=xy(x>0)的图象经过线段OA的端点A,O为原点,作AB垂直于x轴于点B,点B的坐标为(2,0),tan∠AOB=2. 如图,小虎在篮球场上玩,从点O出发,沿着O→A→B→O的路径匀速跑动,能近似刻画小虎所在位置距出发点O的距离S与时间t之间的函数关系的大致图象是( )
如图,小虎在篮球场上玩,从点O出发,沿着O→A→B→O的路径匀速跑动,能近似刻画小虎所在位置距出发点O的距离S与时间t之间的函数关系的大致图象是( )