题目内容
16.(1)如图①,点M为ABCD内一点,请过点M作一条直线将ABCD的面积二等分;(2)如图②,点P为∠AOB内一点,过点P作直线分别交∠AOB的两边于M、N.小明认为当点P为MN的中点时(如图②)时,△OMN的面积最小,你认为小明的说法正确吗?如果正确请给予证明:如果不正确,请说明理由.
(3)如图③,∠AOB=α(0°<α<180°),点P为∠AOB内一点,PC⊥OA于点C,PD⊥OB于点D,PC=3,PD=2,过点P作直线分别交∠AOB的两边于M、N,并将△OMN的面积最小记为S,试探究:在∠α变化过程中S是否存在最小值?如果存在,请求出S的最小值;如果不存在,请说明理由.
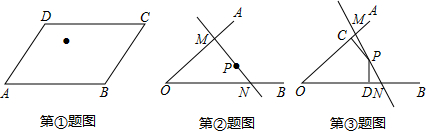
分析 (1)连接AC、BD交于点O,作直线EO,直线EO将矩形ABCD的面积分为相等的两部分;
(2)当直线旋转到点P是MN的中点时S△MON最小,如图2;
(3)如图③中,作PH∥OM交OB于H.因为P是MN中点时,面积最小,推出PM=PN,推出ON=HN,推出OM=2PH,推出当MO⊥OB时,点H与D重合,此时OM=2PD=4此时OM最小,同理可知,此时ON=2PC=6,此时ON的值最小,由此即可解决问题;
解答 解:(1)如图①中,连接AC,BD交于O,过O,M作直线OM,则直线OM将ABCD的面积二等分;
(2)当直线旋转到点P是MN的中点时S△MON最小,如图2,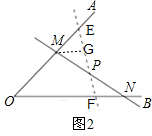
过点P的另一条直线EF交OA、OB于点E、F,设PF<PE,过点M作MG∥OB交EF于G,
易证△MGP≌△NFP,可以推出S四边形MOFG=S△MON.
∵S四边形MOFG<S△EOF,
∴S△MON<S△EOF,
∴当点P是MN的中点时S△MON最小;
(3)如图③中,作PH∥OM交OB于H.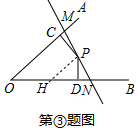
∵P是MN中点时,面积最小,
∴PM=PN,
∴ON=HN,
∴OM=2PH,
∴当MO⊥OB时,点H与D重合,此时OM=2PD=4,此时OM最小,
同理可知,此时ON=2PC=6,此时ON的值最小,
∴△OMN的面积最小值=$\frac{1}{2}$×4×6=12.
点评 本题考查三角形综合题、三角形面积问题、全等三角形的判定和性质、三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

练习册系列答案
相关题目
4.若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点(a,-a),则a的值为( )
| A. | 2或-2 | B. | -2 | C. | 2 | D. | 4 |
11.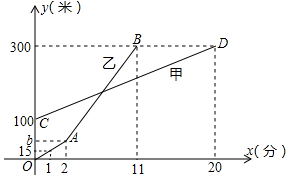 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
 甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )
甲乙两人同时登同一座山,两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示则当乙追上甲时,乙距A地的高度为( )| A. | 165m | B. | 160m | C. | 135m | D. | 120m |
17.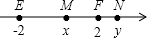 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
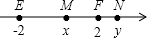 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )| A. | 点E | B. | 点F | C. | 点M | D. | 点N |