题目内容
8.对于二次函数y=a(x-h)2+k,对称轴是x=h,顶点坐标是(h,k).(1)当a>0时,图象开口向上,在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大,当x=h时,y有最大值,是k;
(2)当a<0时,图象开口向下,在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减小,当x=时,y有最小值,是k.
分析 根据二次函数的性质写出对称轴和顶点坐标即可.
解答 解:对于二次函数y=a(x-h)2+k,对称轴是x=h,顶点坐标是(h,k);
(1)当a>0时,图象开口向上,在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大,当x=h时,y有最大值,是k;
(2)当a<0时,图象开口向下,在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减小,当x=h时,y有最小值,是k.
故答案为:x=h,(h,k),向上,减小,增大,h,大,k,向下,增大,减小,h,小,k.
点评 本题考查的是二次函数的性质,熟知二次函数的顶点坐标、二次函数平移的性质等知识是解答此题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.如果$\sqrt{x(x-5)}$=$\sqrt{x}$•$\sqrt{x-5}$成立,则( )
| A. | x≥5 | B. | 0≤x≤5 | C. | x≥0 | D. | x为任意实数 |
19.三边长均为整数,且最大边长为15的三角形共有( )个.
| A. | 64 | B. | 60 | C. | 55 | D. | 49 |
12.关于x的一元二次方程x2-8x+c=0有两个相等的实数根,则c的值为( )
| A. | ±16 | B. | 16 | C. | ±64 | D. | 64 |
9.下列各式中正确的是( )
| A. | ±$\sqrt{9}$=±3 | B. | 16平方根是4 | ||
| C. | (-4)2 的平方根是4 | D. | -(-25)的平方根是-5 |
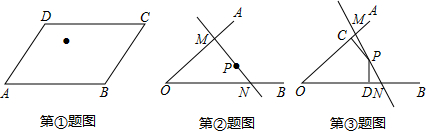
 如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.
如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.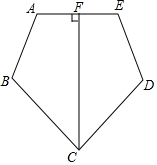 如图,AB=ED,∠B=∠D,BC=CD,且CF⊥AE.求证:AF=EF.
如图,AB=ED,∠B=∠D,BC=CD,且CF⊥AE.求证:AF=EF.