题目内容
14.一个不透明的盒子中有4个小球,小球上面分别标有数字0、1、2、3,每个小球除所标数字不同外其他都相同.小亮先从盒子中随机抽出一个小球,记下数字后不放回,并把其余的球搅匀;再从盒子中随机抽出一个小球记下数字.用画树状图(或列表)的方法,求小亮两次抽出的小球上所标数字之积为偶数的概率.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小亮两次抽出的小球上所标数字之积为偶数的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得: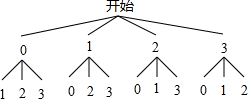
∵共有12种等可能的结果,小亮两次抽出的小球上所标数字之积为偶数的有10种情况,
∴小亮两次抽出的小球上所标数字之积为偶数的概率为:$\frac{10}{12}$=$\frac{5}{6}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.联合国经济和社会事务部于2015年7月29日发布《世界人口展望报告》称,全球人口到2100年将达到112亿(即11 200 000 000人,11 200 000 000这个数据用科学记数法表示为( )
| A. | 11.2×109 | B. | 1.12×1010 | C. | 0.112×1011 | D. | 1.12×1011 |
3.不等式x-1≥1的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
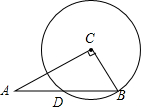 如图,在△ABC中,∠ACB=90°,以点C为圆心,CB为半径的⊙C与边AB交于点D.若点D为AB的中点,AB=6,则⊙C的半径长为3.
如图,在△ABC中,∠ACB=90°,以点C为圆心,CB为半径的⊙C与边AB交于点D.若点D为AB的中点,AB=6,则⊙C的半径长为3.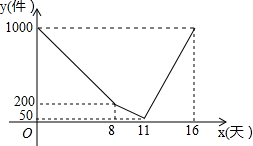 某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)
某厂家开发一种新产品,现有一定的库存量,投入市场试销,在试销期间不生产,试销结束后,厂家开始正式投入生产,当库存量不多时,厂家提高了工作效率.该产品每天的销售量相同时,库存量y(件)与销售天数(x)之间的函数关系如图所示)库存量=原有库存量+日生产量-日销售量)
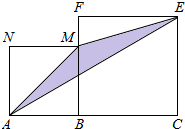 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为