题目内容
5.一个正多边形的内角和是2160°,那么多边形的边数是14,它有77条对角线.分析 设这个多边形的边数为n,根据多边形内角和公式可得:(n-2)×180=1440,再解方程可得n的值;然后再根据n边形从一个顶点出发可引出(n-3)条对角线.从n个顶点出发引出(n-3)条,而每条重复一次,所以n边形对角线的总条数为:$\frac{n(n-3)}{2}$(n≥3,且n为整数)可得答案.
解答 解:设这个多边形的边数为n,由题意得:(n-2)×180=2160,
解得:n=14,
过其中一个顶点可以作对角线条数:14-3=11,
这个多边形对角线总条数:$\frac{14×(14-3)}{2}$=77.
故答案为:14;77.
点评 此题主要考查了多边形内角和公式,以及对角线,关键是掌握多边形内角和定理:(n-2)•180°(n≥3)且n为整数).

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
20.七年级有6个班,每个班平均有n个学生,并且七年级一共有30位老师,则七年级共有师生( )人.
| A. | (6n+30)人 | B. | (6n-30)人 | C. | (30-6n)人 | D. | 6n人 |
10.关于x的一元二次方程ax2-bx+3=0的一个根为x=2,则代数式4b-8a+3的值为( )
| A. | -3 | B. | 3 | C. | 6 | D. | 9 |
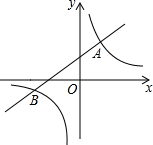 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.