题目内容
6.某校数学兴趣小组用测量仪器测量某大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,试求桥塔AB的高度.(结果精确到0.1米)【参考数据:sin41.5°≈0.663,cos41.5°≈0.719,tan41.5°≈0.885】

分析 在Rt△ADE中利用三角函数即可求得AE的长,则AB的长度即可求解.
解答 解: 过D作DE⊥AB于E,
过D作DE⊥AB于E,
∴DE=BC=50米,
在Rt△ADE中,AE=DE•tan41.5°≈50×0.885≈44.25(米),
∵CD=1米,
∴BE=1米,
∴AB=AE+BE=44.25+1=45.25≈45.3(米),
∴桥塔AB的高度为45.3米.
点评 本题考查仰角的定义,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.下列计算正确的是( )
| A. | a3+a3=a6 | B. | a3•a=a4 | C. | a6÷a2=a3 | D. | (2a2)3=6a5 |
11. 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
 如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )
如图,AB为⊙O的直径,四边形ABCD为⊙O的内接四边形,点P在BA的延长线上,PD与⊙O相切,D为切点,若∠BCD=120°,则∠APD的大小为( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
18.不等式x+5≥1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
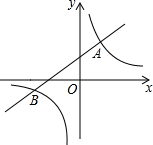 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
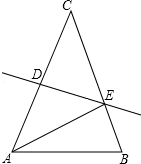 如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.
如图,在三角形纸片△ABC中,AC=BC,∠B=70°,将△ABC沿线段DE所在直线对折,使点A、点C重合,连接AE,则∠AED的度数是50度.