题目内容
已知△BCD为等边三角形,延长BC至A,使CA=BC,连接AD,求∠ADB的度数.
考点:等边三角形的性质,等腰三角形的性质
专题:
分析:由条件可知CD=CA,利用等腰三角形的性质及外角的性质,可求出得∠ADC的度数,进一步可得出∠ADB.
解答:解:∵△BCD为等边三角形,CA=CB,
∴CA=CD,
∴∠A=∠ADC,
∵∠DCB=60°,
∴∠A=∠ADC=30°,
∴∠ADB=∠ADC+∠CDB=30°+60°=90°.
∴CA=CD,
∴∠A=∠ADC,
∵∠DCB=60°,
∴∠A=∠ADC=30°,
∴∠ADB=∠ADC+∠CDB=30°+60°=90°.
点评:本题主要考查等边三角形及等腰三角形的性质,由条件得出∠A=∠ADC=30°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
-1的整数部分为a,小数部分为b,则(
+a)(b+1)=( )
| 11 |
| 11 |
| A、5 | B、6 | C、7 | D、8 |
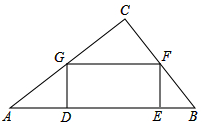 内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.