题目内容

试判断当x取何值时，2x2+4x+1有最小值，并求出最小值．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：直接利用配方法求出2x2+4x+1的最小值即可．
解答：解：2x2+4x+1
=2（x+1）2-1，
故当x=-1时，2x2+4x+1有最小值-1．
点评：此题主要考查了配方法的应用，正确配方得出是解题关键．
练习册系列答案
相关题目
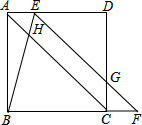如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连接EF与边CD相交于点G，连接BE与对角线AC相交于点H，AE=CF，BE=EG．
（1）求证：EF∥AC；
（2）求∠BEF大小；
（3）若EB=4，则△BAE的面积为
 
．
已知关于x的方程x2-kx+6=0的一个解与方程4x+12=0的解相同．
（1）求k的值；
（2）求方程x2-kx+6=0的另一个解．
已知长方形的长是宽的3倍，其面积为540cm2，求这个长方形的周长．（精确到0.1cm）
已知△BCD为等边三角形，延长BC至A，使CA=BC，连接AD，求∠ADB的度数．
某出租车一天下午以鼓楼为出发点在东西方向营运，向东为正，向西为负，行车里程依先后次序记录如下（单位：km）：+9，-3，-5，+4，-8，+6，-3，-6，-4，+10．
（1）将最后一位乘客送到目的地时，出租车离鼓楼出发点多远？在鼓楼的什么方向？
（2）若每千米的价格为2.4元，司机这个下午的营业额是多少？
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|． 利用数形结合思想回答下列问题：

（1）数轴上表示1和5两点之间的距离是
 
，数轴上表示2和-1的两点之间的距离是
 
；
（2）数轴上表示x和-1的两点之间的距离表示为
 
；
（3）若x表示一个有理数，且-4＜x＜2，则|x-2|-|x+4|=
 
；
（4）利用数轴求出|x+3|+|x+4|的最小值，并写出此时x可取哪些整数值？
阅读下面的文字，解答问题．
大家知道
2
是无理数，而无理数是无限不循环小数，因此
2
的小数部分我们不可能全部地写出来，于是小明用
2
-1来表示
2
的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理，因为
2
的整数部分是1，将这个数减去其整数部分，差就是小数部分． 
请解答：已知12+
5
=x+y，其中x是整数，且0＜y＜1，求x-y+
5
的平方根．
若a与-
5
互为倒数，那么a是（　　）
A、-
5
B、
5
C、
5
5
D、-
5
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网