题目内容
若△ABC三边长满足下列条件,判断△ABC是不是直角三角形?若是,请说明哪个教角是直角.
(1)BC=
,AB=
,AC=1;
(2)△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a=n2-1,b=2n,c=n2+1(n>1)
(1)BC=
| 3 |
| 4 |
| 5 |
| 4 |
(2)△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a=n2-1,b=2n,c=n2+1(n>1)
考点:勾股定理的逆定理
专题:
分析:(1)通过判断,判断BC2+AC2=AB2是否成立,利用勾股定理的逆定理即可判断;
(2)通过判断,判断a2+b2=c2是否成立,利用勾股定理的逆定理即可判断.
(2)通过判断,判断a2+b2=c2是否成立,利用勾股定理的逆定理即可判断.
解答:解:(1)∵(
)2+12=
=(
)2,
∴BC2+AC2=AB2.
∴△ABC是直角三角形;
(2)∵(n2-1)2+(2n)2=n4+2n2+1=(n2+1)2,
∴a2+b2=c2,
∴△ABC是直角三角形.
| 3 |
| 4 |
| 25 |
| 16 |
| 5 |
| 4 |
∴BC2+AC2=AB2.
∴△ABC是直角三角形;
(2)∵(n2-1)2+(2n)2=n4+2n2+1=(n2+1)2,
∴a2+b2=c2,
∴△ABC是直角三角形.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
运用等式性质进行的变形,不正确的是( )
| A、如果a=b,那么a-c=b-c | ||||
| B、如果a=b,那么2a=b+a | ||||
C、如果a=b,那么
| ||||
| D、如果ax=bx,那么a=b |
如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
| ||||
| E、? | ||||
| F、? |
点A的坐标是(1,1),若点B在坐标轴上,且△ABO是等腰三角形,则点B的坐标不可能是( )
| A、(2,0) |
| B、(0.5,0) |
| C、(1,0) |
| D、(0,1) |
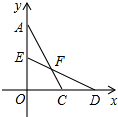 平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.
平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.