题目内容
已知一个小组有若干人，新年互送贺卡一张，全组共送了42张，则这个小组有 人．
考点：一元二次方程的应用
专题：
分析：每个人都要送给他自己以外的其余人，等量关系为：人数×（人数-1）=42，把相关数值代入计算即可．
解答：解：设这个小组有x人．
由题意得：x（x-1）=42，
解得x1=7，x2=-6（不合题意，舍去）．
即这个小组有7人．
故答案为：7．
由题意得：x（x-1）=42，
解得x1=7，x2=-6（不合题意，舍去）．
即这个小组有7人．
故答案为：7．
点评：本题考查一元二次方程的应用，得到互送贺卡总张数的等量关系是解决本题的关键，注意理解本题中互送的含义，这不同于直线上点与线段的数量关系．
练习册系列答案
阅读快车系列答案
相关题目
已知a，b，c的关系如图所示，化简|a-b|+|a+b|-|c|=如果点C是线段AB的黄金分割点（AC＞BC），则下列比例式正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
| ||||
| E、？ | ||||
| F、？ |
点A的坐标是（1，1），若点B在坐标轴上，且△ABO是等腰三角形，则点B的坐标不可能是（ ）
| A、（2，0） |
| B、（0.5，0） |
| C、（1，0） |
| D、（0，1） |
方程
+
+
+
+
=18的解是（ ）
| x-2 |
| 3 |
| x-3 |
| 5 |
| x-2 |
| 7 |
| x-5 |
| 9 |
| x-1 |
| 11 |
| A、x=-32 | B、x=32 |
| C、x=-23 | D、x=23 |
已知抛物线y=-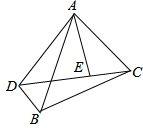
如图，△ADE与△ABC有公共顶点A，∠BAD=∠CAE．