题目内容
17.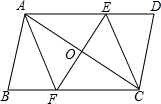 已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是EF⊥AC(直接写出这个条件).
分析 (1)根据平行四边形的性质可得AD∥BC,根据平行线的性质可得∠EAO=∠FCO,然后再加上条件AO=CO,对顶角∠AOE=∠FOC可利用ASA证明△AOE≌△COF;
(2)根据(1)的证明可得EF⊥AC多余.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠FOC}\end{array}\right.$,
∴△AOE≌△COF(ASA);
(2)由(1)的证明可得EF⊥AC多余.
故答案为:EF⊥AC.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形两组对边分别平行.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
7. 如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有( )
如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有( )
 如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有( )
如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有( )| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
 如图,已知∠2+∠3=180°,∠3=∠4=45°,则∠1的度数为45°.
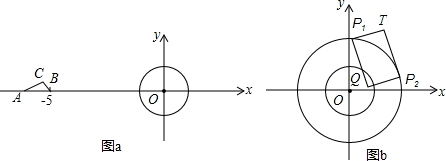
如图,已知∠2+∠3=180°,∠3=∠4=45°,则∠1的度数为45°. 如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,求这个一次函数的表达式及它与x轴的交点.
如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,求这个一次函数的表达式及它与x轴的交点.