题目内容
2. 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图:若CD=AC,∠A=50°,则∠ACB的度数为105°.
①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
分析 根据要求先画出图形,利用等腰三角形的性质以及三角形外角定理求出∠CDB和∠ACD即可.
解答 解:直线MN如图所示:
∵MN垂直平分BC,
∴CD=BD,
∴∠DBC=∠DCB
∵CD=AC,∠A=50°,
∴∠CDA=∠A=50°,
∵∠CDA=∠DBC+∠DCB,
∴∠DCB=∠DBC=25°,∠DCA=180°-∠CDA-∠A=80°,
∴∠ACB=∠CDB+∠ACD=25°+80°=105°.
故答案为105°.
点评 本题考查基本作图、垂直平分线的性质、三角形的外角定理、等腰三角形的性质等知识,解题的关键是灵活应用这些性质解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (-a3)2=a9 | D. | (-a2)3=-a6 |
7.不等式2x+4≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
11.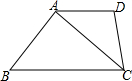 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )| A. | 9$\sqrt{7}$ | B. | 12 | C. | 8 | D. | 8$\sqrt{3}$ |
 如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是10.
如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是10.