题目内容
1.求证:无论k为何值,y2+2xy-x2+2x-2ky+k2+1都不能分解成两个一次因式的乘积.分析 运用反证法,假设结论成立,即为(ax+by+e)(cx+dy+f),展开式子对比探讨得出答案即可.
解答 证明:运用反证法,假设结论成立,即为(ax+by+e)(cx+dy+f)
展开式得
(ax+by+e)(cx+dy+f)=acx2+bdy2+(af+ce)x+(ad+bc)xy+(bf+de)y+ef
由原式原式可知
ac=-1①
bd=1②
af+ce=2③
bc+ad=-2④
bf+de=-2k⑤
ef=k2+1⑥
由②、⑥式得d=$\frac{1}{b}$,e=$\frac{1}{f}$(k2+1)
将d、e分别带入5式 得
bf+(k2+1)$\frac{1}{bf}$=-2k
整理得到
(bf+k)2=-1无解,
故原假设不成立,
故无论k为何值,y2+2xy-x2+2x-2ky+k2+1不能分解为两个一次因式的乘积.
点评 此题考查了因式分解d的实际运用,熟练掌握多项式乘以多项式法则是解本题的关键.

练习册系列答案
相关题目
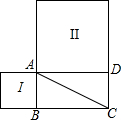 如图,矩形ABCD的对角线AC=6cm,分别以AB和AD为一边向外作正方形Ⅰ和Ⅱ,则正方形Ⅰ和Ⅱ的面积之和是多少?
如图,矩形ABCD的对角线AC=6cm,分别以AB和AD为一边向外作正方形Ⅰ和Ⅱ,则正方形Ⅰ和Ⅱ的面积之和是多少?