Question

16．求证：三角形三条边的垂直平分线相交于一点，并且这个点到三个顶点的距离相等．

Answer 1

分析 根据题意画出图形，根据线段垂直平分线的性质求解即可．

解答 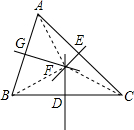已知：△ABC
求证：AB、BC、AC三边的垂直平分线相交于点F，且FA=FB=FC，
证明：如图，作AB边的垂直平分线FG，FG交AB于点G，作BC边的垂直平分线FD，FD交BC边于点D，
∵点F是AB边垂直平线上的一点，
∴FA=FB，
同理可得，FB=FC，
∴FA=FB=FC（等量代换），
∴点F在线段AC的垂直平分线上，
∴AB、BC、AC三边的垂直平分线相交于一点P，且这一点到三个顶点的距离相等．

点评 本题考查的是线段垂直平分线的性质，即线段的垂直平分线上的点到线段的两个端点的距离相等．