题目内容
5.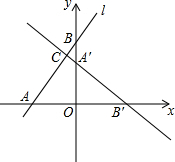 如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.(1)求直线A′B′的解析式;
(2)若直线A′B′与直线l相交于点C,求△A′BC的面积.
分析 (1)先根据一次函数的解析式求出AB两点的坐标,再由图形旋转的性质求出A′、B′的坐标,用待定系数法求出直线A′B′的解析式即可;
(2)直接根据A′、B、C的坐标,利用三角形的面积公式进行计算即可.
解答 解:(1)∵令x=0,则y=4,令y=0,则x=-3,
∴A(-3,0),B(0,4),
由图形旋转的性质可知,A′( 0,3),B′( 4,0),
设过A′( 0,3),B′( 4,0)的解析式为y=kx+b(k≠0)
则$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$.
故此直线的解析式为:y=-$\frac{3}{4}$x+3;
(2)∵过A′,B′两点的解析式为:y=-$\frac{3}{4}$x+3,
∴$\left\{\begin{array}{l}{y=-\frac{3}{4}x+3}\\{y=\frac{4}{3}x+4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{12}{25}}\\{y=\frac{84}{25}}\end{array}\right.$,
∴C(-$\frac{12}{25}$,-$\frac{84}{25}$),
∴S△A’BC=$\frac{1}{2}$|A′B|×|xC|=$\frac{1}{2}$×1×$\frac{12}{25}$=$\frac{6}{25}$.
点评 本题考查的是一次函数的图象与及几何变换、一次函数的性质及三角形的面积公式,根据题意求出直线A′B′的解析式是解答此题的关键.

| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\frac{2+\sqrt{2}}{2}$ |
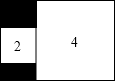 如图,在矩形内有两个相邻的正方形,面积分别为2和4,则图中阴影部分的面积是2$\sqrt{2}$-2.
如图,在矩形内有两个相邻的正方形,面积分别为2和4,则图中阴影部分的面积是2$\sqrt{2}$-2.



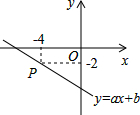 在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
在教学活动中我们知道,任何一个二元一次方程的图象都是一条直线,如图,已知直线y=ax-6过点P(-4,-2),则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.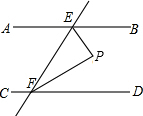 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.