题目内容
14.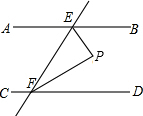 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,求∠P.
分析 由AB∥CD,可知∠BEF与∠DFE互补,由角平分线的性质可得∠PEF+∠PFE=90°,由三角形内角和定理可得∠P=90度.
解答 解:∵AB∥CD
∴∠BEF+∠DFE=180°
又∵∠BEF的平分线与∠DFE的平分线相交于点P
∴∠PEF=$\frac{1}{2}$∠BEF,∠PFE=$\frac{1}{2}$∠DFE
∴∠PEF+∠PFE=$\frac{1}{2}$(∠BEF+∠DFE)=90°
∵∠PEF+∠PFE+∠P=180°
∴∠P=90°.
点评 本题考查了平行线的性质、角平分线的定义、三角形内角和定理,熟练掌握这些定理是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
9.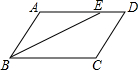 如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
 如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )| A. | 30° | B. | 60° | C. | 120° | D. | 以上答案都不对 |
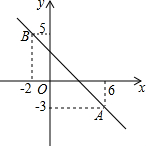 如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).
如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).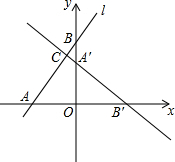 如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.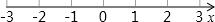
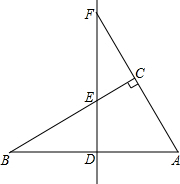 如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.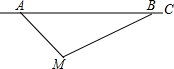 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.