题目内容
17.电子跳蚤游戏盘为△ABC,AB=8a,BC=10a,如果电子跳蚤开始时在BC边上P0点,BP0=4a,第一步,跳蚤跳到AC边上P1点,且CP1=CP0;第二步,跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步,跳蚤从P2跳到BC边上P3点,且BP1=BP2;…跳蚤按上述规则跳下去,第2001次落到点P2001上,请计算P0与P2001之间的距离为a.分析 首先根据题意,分别计算电子跳蚤的位置和三角形的顶点的距离,找到循环的规律:经过6次跳,电子跳蚤回到起跳点.根据这一规律确定第2001次落点的位置,从而确定P0与P2001之间的距离.
解答 解:因为BP0=4a,根据题意,CP0=10a-4a=6a,
第一步从P0到P1,CP1=CP0=6a;AP1=9a-6a=3a,
第二步从P1到P2,AP2=AP1=3a;BP2=8a-3a=5a,
第三步从P2到P3,BP3=BP2=5a;CP3=10a-5a=5a,
第四步从P3到P4,CP4=CP3=5a;AP4=9a-5a=4a,
第五步从P4到P5,AP5=AP4=4a;BP5=8a-4a=4a,
第六步从P5到P6,BP6=BP5=4a;
由此可知,P6点与P0点重合,又因为2001=6×333+3,所以P2001点与P3点重合,则P0与P2001之间的距离为P0P3=10a-4a-5a=a.
故答案为:a.
点评 本题是一道探索规律题,根据题意计算出前几步直到发现循环规律,然后进行推演是此类题目的一般解题思路.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若一个点的横坐标与纵坐标互为相反数,则此点一定在( )
| A. | 原点 | B. | 横轴上 | ||
| C. | 第二、四象限角平分线上 | D. | 第一、三象限角平分线上 |
9.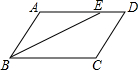 如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
 如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )
如图,?ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( )| A. | 30° | B. | 60° | C. | 120° | D. | 以上答案都不对 |
7.某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
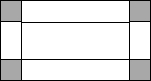 如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.
如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.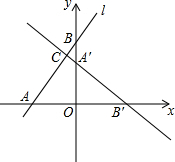 如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.