题目内容
13.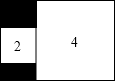 如图,在矩形内有两个相邻的正方形,面积分别为2和4,则图中阴影部分的面积是2$\sqrt{2}$-2.
如图,在矩形内有两个相邻的正方形,面积分别为2和4,则图中阴影部分的面积是2$\sqrt{2}$-2.
分析 根据两个正方形的面积,利用算术平方根定义求出各自的边长,即可确定出阴影部分即可.
解答 解:由相邻两个正方形的面积分别为2和4,得到边长为$\sqrt{2}$和2,
则阴影部分面积S=$\sqrt{2}$×(2-$\sqrt{2}$)=2$\sqrt{2}$-2,
故答案为:2$\sqrt{2}$-2
点评 此题考查了算术平方根,熟练掌握算术平方根的定义是解本题的关键.

练习册系列答案
相关题目
3.下列标识中,既是轴对称图形,又是中心对称图形的是( )
| A. | 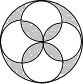 | B. | 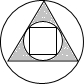 | C. |  | D. |  |
1.下列说法中错误的是( )
| A. | 成中心对称的两个图形全等 | |
| B. | 成中心对称的两个图形中,对称点的连线被对称轴平分 | |
| C. | 中心对称图形的对称中心是对称点连线的中心 | |
| D. | 中心对称图形绕对称中心旋转180°后,都能与自身重合 |
8.若一个点的横坐标与纵坐标互为相反数,则此点一定在( )
| A. | 原点 | B. | 横轴上 | ||
| C. | 第二、四象限角平分线上 | D. | 第一、三象限角平分线上 |
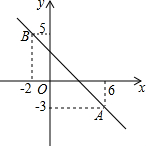 如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).
如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).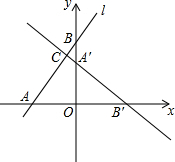 如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
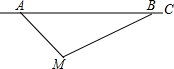 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.