题目内容
14.一个底面为正三角形,侧棱与底面垂直的棱柱,其三视图如图所示,则这个棱柱的体积为36$\sqrt{3}$.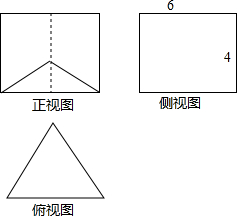
分析 由三视图判断几何体为三棱柱,把相关数据代入体积公式计算可得答案.
解答 解:三视图复原的几何体是三棱柱,底面是正三角形,则边长为6,高为3$\sqrt{3}$,
由三视图可得棱柱高为4,
它的体积:V=Sh=$\frac{1}{2}$×6×3$\sqrt{3}$×4=36$\sqrt{3}$;
故答案为:36$\sqrt{3}$.
点评 本题考查了由三视图判断几何体,用到的知识点是三棱柱的体积公式,关键是判断三视图的数据所对应的几何量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
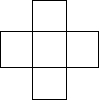 如图是一个由5个相同的正方形组成的十字形的纸片,把这一纸片沿一条直线裁成两部分,然后把其中的一部分再沿着另一条直线截成两部分,使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形.请在图中画出分割线及拼接后的图形.
如图是一个由5个相同的正方形组成的十字形的纸片,把这一纸片沿一条直线裁成两部分,然后把其中的一部分再沿着另一条直线截成两部分,使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形.请在图中画出分割线及拼接后的图形.
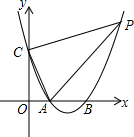 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标. 如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.
如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.