题目内容
4. 如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.
如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.
分析 根据平角的知识可求出∠DED′的度数,再由折叠的性质可得出∠D′EF=∠DEF=$\frac{1}{2}$∠DED′,从而根据平行线的性质可得出∠EFB的度数.
解答 解:∵∠AED′=40°,
∴∠DED′=180°-40°=140°,
又由折叠的性质可得,∠D′EF=∠DEF=$\frac{1}{2}$∠DED′,
∴∠DEF=70°,
又∵AD∥BC,
∴∠EFB=70°.
故答案为:70.
点评 此题考查了翻折变换的知识,解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=$\frac{1}{2}$∠DED′,难度一般.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
9. 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则△PAB的周长为( )| A. | 5cm | B. | 10cm | C. | 20cm | D. | 15cm |
13. 如图,该图案对称轴的条数是( )
如图,该图案对称轴的条数是( )
 如图,该图案对称轴的条数是( )
如图,该图案对称轴的条数是( )| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |

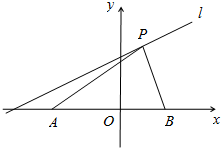 已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.
已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围. 如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.
如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.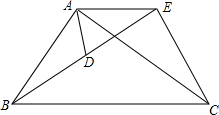 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.