题目内容
7. 如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.
如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.探究(一)
(1)x=$\frac{3}{2}$时,点B'落在AC上,此时折痕EF=$\frac{5}{2}$;
(2)x=$\frac{75}{32}$时,点B'落在AD上.
探究(二)
当点B落在矩形区域上(含边界),设△B'EF的面积为S.
求S与x之间的函数关系式,并求出S的最大值.
分析 探究一:(1)只要证明EF是△ABC的中位线即可;
(2)如图2中,设BB′交EF于O,交AC于K.由△ABK∽△B′BA,推出$\frac{BK}{BA}$=$\frac{AB}{BB′}$,推出BB′=$\frac{15}{4}$,推出OB=OB′=$\frac{15}{8}$,由△BOE∽△BKA,可得$\frac{BO}{BK}$=$\frac{BE}{BA}$,可得BE=$\frac{75}{32}$;
探究二:由EF∥AC,可得$\frac{BE}{BA}$=$\frac{BF}{AC}$,推出BF=$\frac{4}{3}$x,当B′在AD上时,△EFB′的面积最大;
解答 解:探究(一):
(1)如图1中,设EF交BB′于O.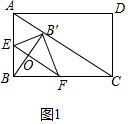
∵B、B′关于EF对称,
∴EF垂直平分BB′,
∴OB=OB′,
∵EF∥AC,
∴BE=AE=$\frac{3}{2}$,BF=FC,
∴EF=$\frac{1}{2}$AC,易知AC=5,
∴EF=$\frac{5}{2}$.
故答案为$\frac{3}{2}$,$\frac{5}{2}$.
(2)如图2中,设BB′交EF于O,交AC于K.
∵$\frac{1}{2}$•AC•BK=$\frac{1}{2}$•AB•BC,
∴BK=$\frac{12}{5}$,
∵△ABK∽△B′BA,
∴$\frac{BK}{BA}$=$\frac{AB}{BB′}$,
∴BB′=$\frac{15}{4}$,
∴OB=OB′=$\frac{15}{8}$,
∵△BOE∽△BKA,
∴$\frac{BO}{BK}$=$\frac{BE}{BA}$,
∴BE=$\frac{75}{32}$.
故答案为$\frac{75}{32}$.
探究(二)
∵EF∥AC,
∴$\frac{BE}{BA}$=$\frac{BF}{AC}$,
∴BF=$\frac{4}{3}$x,
∴S=$\frac{1}{2}$•x•$\frac{4}{3}$x=$\frac{2}{3}$x2(0<x≤$\frac{75}{32}$),
当x=$\frac{75}{32}$时,S的值最大,最大值为$\frac{1875}{512}$.
点评 本题考查翻折变换、矩形的性质、相似三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题.

 如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )
如图所示是某长方体形状包装盒的表面展开图,根据图中的数据,该包装盒的容积是(包装盒材料的厚度忽略不计)( )| A. | 40×70×80 | B. | 80×80×40 | C. | 40×40×70 | D. | 70×70×80 |
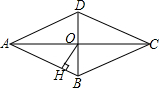 如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则菱形的面积为24,点O到边AB的距离OH=2.4.
如图,菱形ABCD的对角线AC、BD相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则菱形的面积为24,点O到边AB的距离OH=2.4.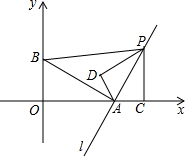 如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2).
如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为P(5,2),p(8,8),P(0,-8),P(3,-2). 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.