题目内容
10．
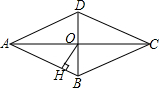如图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则菱形的面积为24，点O到边AB的距离OH=2.4．
分析 首先利用菱形的性质得出AO=4，BO=3，∠AOB=90°，进而利用勾股定理得出AB的长，再利用三角形面积公式求出HO的长．
解答 解：∵菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，
∴菱形的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}×$8×6=24；
∴AO=4，BO=3，∠AOB=90°，
∴在Rt△AOB中，AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5，
∵OH⊥AB，
∴HO×AB=AO×BO，
∴HO=$\frac{AO•BO}{AB}$=2.4．
故答案为：24，2.4．
点评 此题主要考查了菱形的性质以及勾股定理等知识，得出AB的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．某总公司为了评价甲、乙两个分公司去年的产值，统计了这两个分公司去年12个月的产值（单位：万元）情况，分别如图所示：
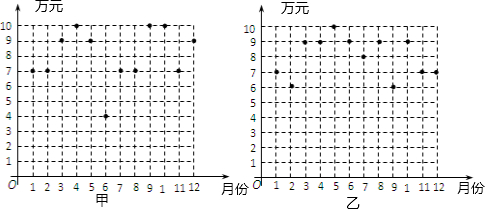
（1）利用上图中的信息，完成下表：
（2）假若你是公司的总经理，请你请从以下三个不同的角度对两个分公司的产值进行分析，对两个分公司做出评价；
①从平均数和众数相结合看（分析哪个公司产值好些）；
②从平均数和中位数相结合看（分析哪个公司产值好些）．
③从平均数和方差相结合看（分析哪个公司产值好些）．
（1）利用上图中的信息，完成下表：
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲 | 8 | 8 | 7 | 3 |
| 乙 | 8 | 8.5 | 9 | 1.5 |
①从平均数和众数相结合看（分析哪个公司产值好些）；
②从平均数和中位数相结合看（分析哪个公司产值好些）．
③从平均数和方差相结合看（分析哪个公司产值好些）．
如图，若AE是△ABC边BC上的高，∠EAC的平分线AD交BC于D，若∠DAC=25°，求∠C的度数．
5．用相同边长的正三角形和正方形进行镶嵌，若每一个顶点周围有m个正三角形和n个正方形．则m，n满足的关系是（ ）
| A． | 2m+3n=12 | B． | m+n=7 | C． | 2m+n=6 | D． | m+2n=6 |
如图1，矩形ABCD，AB=3，BC=4，E，F分别在AB，BC边上，且EF∥AC；将△BEF沿EF折叠，得△B'EF，设BE=x．