题目内容
2.解方程$\frac{x}{x-3}+2=\frac{3}{3-x}$,并说明“去分母”这一步骤的作用.分析 方程两边都乘以x-3得出整式方程,求出方程的解,再进行检验即可.
解答 解:方程两边都乘以x-3得:x+2(x-3)=-3,
解得:x=1,
检验:∵当x=1时,x-3≠0,
∴x=1是原方程的解,
即原方程的解为x=1;
“去分母”这一步骤的作用是:把分式方程转化成整式方程.
点评 本题考查了解分式方程,能把分式方程转化成整式方程是解此题的关键,注意:解分式方程一定要进行检验.

练习册系列答案
相关题目
5.用相同边长的正三角形和正方形进行镶嵌,若每一个顶点周围有m个正三角形和n个正方形.则m,n满足的关系是( )
| A. | 2m+3n=12 | B. | m+n=7 | C. | 2m+n=6 | D. | m+2n=6 |
10.已知下列各式:①2x-3y②$\frac{1}{x}$+y=2③xy+y=-2④x+y=z-2⑤$\frac{x+1}{2}$=1-$\frac{y}{3}$⑥x=y.其中二元一次方程的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
12.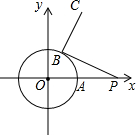 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )| A. | 2$\sqrt{2}$π | B. | 4π | C. | 4$\sqrt{2}$π | D. | 6π |
 如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.
如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.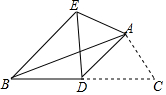 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置,求∠EBC的度数.