题目内容
17. 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED、EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=2,BC=5,则EF的值是$\sqrt{10}$.
分析 如图,首先运用翻折变换的性质求出CF、DF的长度,证明∠DEC=90°;运用射影定理求出EF的长度,即可解决问题.
解答  解:如图,由翻折变换的性质得:
解:如图,由翻折变换的性质得:
CF=CB=5,DF=DA=2,∠EFC=∠B=90°;
∠AED=∠FED,∠BEC=∠FEC,
∴∠DEC=$\frac{1}{2}$180°=90°,即EF⊥CD,
∴由射影定理得:EF2=CF•DF,
∴EF=$\sqrt{10}$,
故答案为$\sqrt{10}$.
点评 该题主要考查了翻折变换的性质、射影定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、射影定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
8.已知一个正数的两个平方根分别为2a-5和1-a,则这个正数为( )
| A. | 3 | B. | 4 | C. | 9 | D. | 16 |
5.由于微电子技术的不断进步,可以在300平方毫米的芯片上集成6亿个元件,平均每个元件约占( )
| A. | 5×10-7毫米2 | B. | 5×10-8毫米2 | C. | 2×106毫米2 | D. | 2×107毫米2 |
12.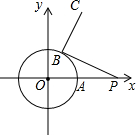 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )| A. | 2$\sqrt{2}$π | B. | 4π | C. | 4$\sqrt{2}$π | D. | 6π |
2.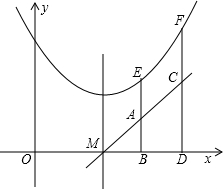 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
 如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.
如图1,矩形ABCD,AB=3,BC=4,E,F分别在AB,BC边上,且EF∥AC;将△BEF沿EF折叠,得△B'EF,设BE=x.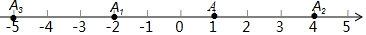 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33. 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.