Question

3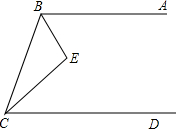．如图，已知∠E=90°，BE平分∠ABC，CE平分∠BCD，求证：AB∥CD．

Answer 1

分析 根据角平分线的性质得出得出∠1=∠ABE，∠2=∠ECD，进而求出∠ABE+∠1+∠2+∠ECD=180°，再利用同旁内角互补两直线平行进而得出答案．

解答 解：AB∥CD，理由如下：
∵BE平分∠ABC，CE平分∠BCD，
∴∠1=∠ABE，∠2=∠ECD，
∵∠E=90°，
∴∠1十∠2=90°，
∴∠ABE+∠1+∠2+∠ECD=180°，
即∠ABC+∠BCD=180°，
∴AB∥CD．

点评 此题主要考查了平行线的判定以及角平分线的性质等知识，熟练掌握平行线的判定是解题关键．