题目内容
18. (1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;
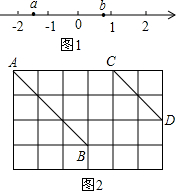
(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;(2)已知实数a、b在数轴上的位置如图1所示,化简下列算式:
$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$+$\sqrt{(a+b)^{2}}$;
(3)如图2,在6×4正方形网格中,每个小正方形的边长都是1.
①分别求出线段AB、CD的长度;
②在图中画出线段EF,使得EF的长为$\sqrt{10}$,并判断以AB,CD,EF三条线段能否构成直角三角形,并说明理由.
分析 (1)先化简,再进一步合并即可;
(2)由数轴可知:-2<a<-1,0<b<1,进一步根据二次根式的意义化简,最后合并即可;
(3)①利用勾股定理求得AB、CD的长度即可;
②因为EF的长为$\sqrt{10}$=$\sqrt{{3}^{2}+{1}^{2}}$,由此画出,进一步利用勾股定理逆定理判定即可.
解答 解:(1)原式=4$\sqrt{3}$-2$\sqrt{3}$+12$\sqrt{3}$
=14$\sqrt{3}$;
(2)∵-2<a<-1,0<b<1,
∴原式=b-(a-b)+(a+b)
=b-a+b+a+b
=3b.
(3)①AB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,CD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
②如图,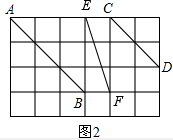
因为AB2=18,CD2=8,EF2=10,AB2,CD2+EF2,
所以AB,CD,EF三条线段能构成直角三角形.
点评 此题考查二次根式的化简求值,勾股定理与逆定理的运用,二次根式的混合运算需先化简再求值,正确理解掌握勾股定理解决数形结合的问题.

练习册系列答案
相关题目
6.组数为三角形的三边.其中,能构成直角三角形的是( )
| A. | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | B. | 32、42、52 | C. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D. | 3k、4k、5k(k≠0) |
13.若二次函数y=ax2+bx+c的x与y的部分对应值如表,则当x=-1时,y的值为-3.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
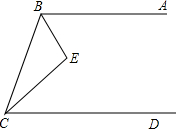 如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD.
如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD.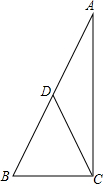 如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.
如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.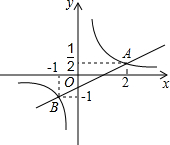 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.