题目内容
15.若菱形的面积为24,一条对角线长为8,则另一条对角线长为6,边长为5.分析 先由菱形面积=$\frac{1}{2}$AC•BD,求出另一条对角线长;再根据菱形的性质求出OA、OB,由勾股定理即可求出边长.
解答 解:如图所示: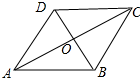 ∵菱形ABCD的面积=$\frac{1}{2}$AC•BD=24,AC=8,
∵菱形ABCD的面积=$\frac{1}{2}$AC•BD=24,AC=8,
∴BD,=6;
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5;
故答案为:6;5.
点评 本题考查了菱形的性质、面积的计算方法以及勾股定理的运用;熟练掌握菱形的性质和面积的计算方法是解决问题的关键.

练习册系列答案
相关题目
6.组数为三角形的三边.其中,能构成直角三角形的是( )
| A. | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | B. | 32、42、52 | C. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D. | 3k、4k、5k(k≠0) |
5.下列多项式的乘法运算可以用平方差公式计算的是( )
| A. | -(2a-3b)(3b-2a) | B. | (2a-3b)(3a+2b) | C. | (2a+3b)(-2a-3b) | D. | (2a+3b)(3b-2a) |
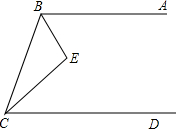 如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD.
如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD.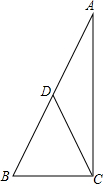 如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.
如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长. 如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.
如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.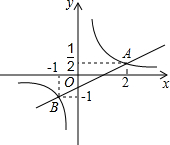 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.