题目内容
12. 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
分析 利用平行四边形的性质结合四边形内角和得出∠EAF的度数,再利用锐角三角函数关系求出?ABCD的周长.
解答 解:∵四边形ABCD是平行四边形,
∴∠BAD=∠C=120°,则∠B=∠D=60°,
∵∠AEC=∠AFC=90°,
∴∠EAF=60°,
∴cos60°=$\frac{BE}{AB}$,则AB=$\frac{BE}{cos60°}$=$\frac{2}{\frac{1}{2}}$=4,
cos60°=$\frac{DF}{AD}$,则AD=$\frac{3}{\frac{1}{2}}$=6,
故?ABCD的周长为:(4+6)×2=20.
故答案为:60°,20.
点评 此题主要考查了平形四边形的性质以及锐角三角函数关系,正确得出∠B的度数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在一个不透明的袋子中装有4个白球和3个黑球,它们除了颜色外都相同,随机从中摸出2个球,属于不可能事件的是( )
| A. | 摸到2个白球 | B. | 摸到2个黑球 | ||
| C. | 摸到1个白球,1个黑球 | D. | 摸到1个黑球,1个红球 |
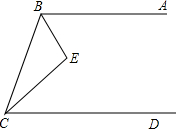 如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD.
如图,已知∠E=90°,BE平分∠ABC,CE平分∠BCD,求证:AB∥CD. 如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.
如图,AB∥EF,BC∥FG,BM、FN分别是∠ABC、∠EFG的三等分线且靠近AB、EF,求证:BM∥FN.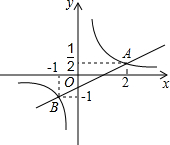 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于A(2,$\frac{1}{2}$),B(-1,1)两点.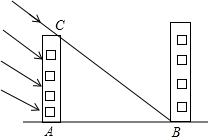 冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?
冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?
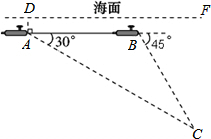 如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).