题目内容
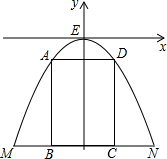 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.考点:二次函数的应用
专题:
分析:首先求出抛物线解析式,进而得出D点纵坐标,即可得出答案.
解答:解:由题意可得:N点坐标为:(2,-4),D(x,-1),
设抛物线解析式为:y=ax2,
则-4=4a,
解得:a=-1,
故函数解析式为:y=-x2,
当y=-1,则-1=-x2,
解得:x1=-1,x2=1,
故AD=BC=2,
则这个“支撑架”的周长为:3×2+2×2=10(m).
答:这个“支撑架”的周长为10m.
设抛物线解析式为:y=ax2,
则-4=4a,
解得:a=-1,
故函数解析式为:y=-x2,
当y=-1,则-1=-x2,
解得:x1=-1,x2=1,
故AD=BC=2,
则这个“支撑架”的周长为:3×2+2×2=10(m).
答:这个“支撑架”的周长为10m.
点评:此题主要考查了二次函数的应用,根据题意得出抛物线解析式是解题关键.

练习册系列答案
相关题目
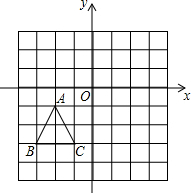 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3). 某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示:
某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示: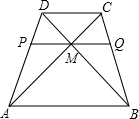 过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.
过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比. 如图.大桥的圆拱的跨度CD为80米,拱高EF为20米,求这个圆拱所在圆的直径.
如图.大桥的圆拱的跨度CD为80米,拱高EF为20米,求这个圆拱所在圆的直径.