题目内容
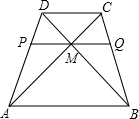 过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.
过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.考点:位似变换
专题:常规题型
分析:由于PM∥AB∥CD,根据相似三角形的判定易得△DPM∽△DAB,△CQM∽△CBA,△APM∽△ADC,△BQM∽△BCD,再利用相似的性质求出它们的相似比,
然后根据位似图形、位似中心和位似比可判断△DPM和△DAB是位似图形,点D为位似中心,位似比为
;△CMQ和△CAB是位似图形,点C为位似中心,位似比为
;△APM和△ADC是位似图形,点A为位似中心,位似比为
;△BMQ和△BDC是位似图形,点B为位似中心,位似比为
;△MCD和△MAB是位似图形,点M为位似中心,位似比为
.
然后根据位似图形、位似中心和位似比可判断△DPM和△DAB是位似图形,点D为位似中心,位似比为
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:∵PM∥AB,
∴△DPM∽△DAB,相似比=
=
=
,
同理可得△CQM∽△CBA,相似比=
,
∵PM∥CD,
∴△APM∽△ADC,相似比=
=
,
同理可得△BQM∽△BCD,相似比=
,
∵四边形ABCD为梯形,
∴CD∥AB,
∴△MCD∽△MAB,
∵PM∥CD,
∴
=
=
,
∵PM∥AB,
∴
=
,
∴
=
,
∴△DPM和△DAB是位似图形,点D为位似中心,位似比为
;
△CMQ和△CAB是位似图形,点C为位似中心,位似比为
;
△APM和△ADC是位似图形,点A为位似中心,位似比为
;
△BMQ和△BDC是位似图形,点B为位似中心,位似比为
;
△MCD和△MAB是位似图形,点M为位似中心,位似比为
.
∴△DPM∽△DAB,相似比=
| PD |
| DA |
| PD |
| PD+AP |
| 1 |
| 3 |
同理可得△CQM∽△CBA,相似比=
| 1 |
| 3 |
∵PM∥CD,
∴△APM∽△ADC,相似比=
| AP |
| AD |
| 2 |
| 3 |
同理可得△BQM∽△BCD,相似比=
| 2 |
| 3 |
∵四边形ABCD为梯形,
∴CD∥AB,
∴△MCD∽△MAB,
∵PM∥CD,
∴
| PM |
| CD |
| AP |
| AD |
| 2 |
| 3 |
∵PM∥AB,
∴
| PM |
| AB |
| 1 |
| 3 |
∴
| CD |
| AB |
| 1 |
| 2 |
∴△DPM和△DAB是位似图形,点D为位似中心,位似比为
| 1 |
| 3 |
△CMQ和△CAB是位似图形,点C为位似中心,位似比为
| 1 |
| 3 |
△APM和△ADC是位似图形,点A为位似中心,位似比为
| 2 |
| 3 |
△BMQ和△BDC是位似图形,点B为位似中心,位似比为
| 2 |
| 3 |
△MCD和△MAB是位似图形,点M为位似中心,位似比为
| 1 |
| 2 |
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.

练习册系列答案
相关题目
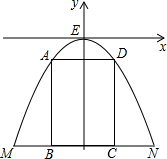 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.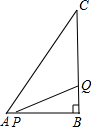 如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2? 如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为
如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为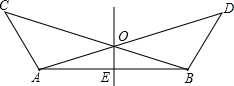 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.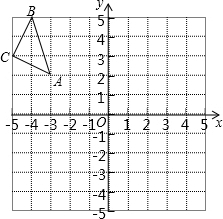 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).