题目内容
 某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示:
某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示:(1)现建立如图所示的平面直角坐标系,试求抛物线的解析式;
(2)若菜农曹大爷身高1.6m,则他在不弯腰的情况下,横向活动的范围最大有几米?
考点:二次函数的应用
专题:
分析:(1)利用待定系数法求出函数解析式进而得出答案;
(2)利用所求函数解析式进而得出y=1.6m时,x的值进而得出答案.
(2)利用所求函数解析式进而得出y=1.6m时,x的值进而得出答案.
解答:解:(1)设抛物线解析式为:y=ax2+c,
将(0,2),(2,0),代入得出:
,
解得:
,
故抛物线的解析式为:y=-
x2+2;
(2)当y=1.6m时,1.6=-
x2+2,
解得:x1=
,x2=-
,
故
-(-
)=
(m),
答:菜农曹大爷身高1.6m,则他在不弯腰的情况下,横向活动的范围最大有
米.
将(0,2),(2,0),代入得出:
|
解得:
|
故抛物线的解析式为:y=-
| 1 |
| 2 |
(2)当y=1.6m时,1.6=-
| 1 |
| 2 |
解得:x1=
2
| ||
| 5 |
2
| ||
| 5 |
故
2
| ||
| 5 |
2
| ||
| 5 |
4
| ||
| 5 |
答:菜农曹大爷身高1.6m,则他在不弯腰的情况下,横向活动的范围最大有
4
| ||
| 5 |
点评:此题主要考查了二次函数的应用,正确求出函数解析式是解题关键.

练习册系列答案
相关题目
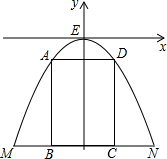 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.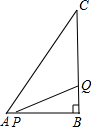 如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=10cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动.点Q到达点C后,点P、Q停止运动.设P、Q从点A、B同时出发,经过多少秒后,△PBQ的面积是10cm2? 如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为
如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为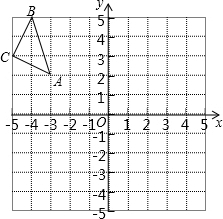 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).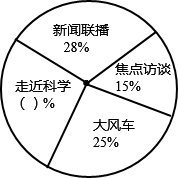 如图是某学校教师喜欢看的电视节目统计图.
如图是某学校教师喜欢看的电视节目统计图.