题目内容
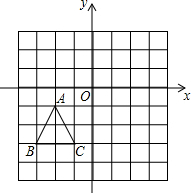 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).①画出△ABC关于x轴对称的△A1B1C1,则点A1的坐标为
②画出△ABC关于原点O对称的△A2B2C2,则四边形A1A2B2B1的面积为
考点:作图-旋转变换,作图-轴对称变换
专题:
分析:①直接作出点A、B、C关于x轴对称的点,然后顺次连接,写出点A1的坐标;
②直接作出点A、B、C关于原点O对称的点,然后顺次连接,根据梯形的面积公式求出四边形A1A2B2B1的面积.
②直接作出点A、B、C关于原点O对称的点,然后顺次连接,根据梯形的面积公式求出四边形A1A2B2B1的面积.
解答: 解:①所作图形如图所示:
解:①所作图形如图所示:
点A1的坐标为(-2,1);
②所作图形如图所示:
四边形A1A2B2B1的面积=
(4+6)×2=10.
故答案为:(-2,1);10.
 解:①所作图形如图所示:
解:①所作图形如图所示:点A1的坐标为(-2,1);
②所作图形如图所示:
四边形A1A2B2B1的面积=
| 1 |
| 2 |
故答案为:(-2,1);10.
点评:本题考查了根据旋转变换和轴对称变换作图,解答本题的关键是根据网格结构做出对应点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 工匠制作某种金属工具要进行材料煅烧和煅造两个工序.即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
工匠制作某种金属工具要进行材料煅烧和煅造两个工序.即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.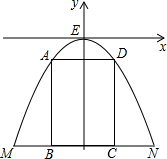 如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长.
如图,某公路隧道横截面为抛物线,其最高点E距离路面4米,底部宽度MN为4米,因维修要搭建一个高度为3米的矩形形状的“支撑架”,已知矩形ABCD的两个顶点A、D在抛物线上,B、C两点在地面MN上,求所需的矩形“支撑架”的周长,为解决这个问题,小明想出了一个方法:以E为坐标原点,MN的中垂线为y轴,建立平面直角坐标系,先求出抛物线的解析式,再解决.请你替小明求出抛物线的解析式,再求出这个“支撑架”的周长. 如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为
如图,在Rt△ABC中,∠C=90°,DE⊥BC,BC=40,CD=10,DE=20,则AC的长为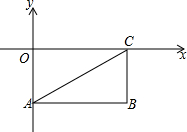 如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.
如图,矩形OABC的两边在坐标轴上,A(0,-2)、C(4,0),连接AC,若点P由点A出发以每秒1个单位的速度沿AB边向B移动,1秒以后点Q也由点A出发以每秒7个单位的速度沿AO、OC、CB边向点B移动,当其中一个点到达终点时,另一个点也停止移动,点P的移动时间为t秒.