题目内容
15.已知:抛物线y=(m-1)x2+mx+m2-4的图象经过原点,且开口向上.(1)确定m的值;
(2)求此抛物线的顶点坐标;
(3)当x取什么值时,y随x的增大而增大?
(4)当x取什么值时,y<0?
分析 (1)图象经过原点,即x=0时,y=0,列方程求解,同时要注意开口向上,即m-1>0;
(2)把得出抛物线的一般式用配方法转化为顶点式,可求顶点坐标;
(3)画抛物线时,要明确表示抛物线与x轴,y轴的交点,顶点坐标及开口方向等;
(4)观察图象,可直接得出y<0时,x的取值范围.
解答 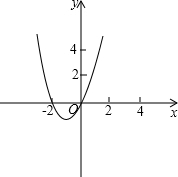 解:(1)由题意得$\left\{\begin{array}{l}{m-1>0}\\{{m}^{2}-4=0}\end{array}\right.$,
解:(1)由题意得$\left\{\begin{array}{l}{m-1>0}\\{{m}^{2}-4=0}\end{array}\right.$,
解得m=2;
(2)∵抛物线解析式为y=x2+2x=(x+1)2-1,
∴顶点坐标是(-1,-1);
(3)抛物线如图如图所示;由图可知,x>-1时,y随x的增大而增大;
(4)由图可知,当-2<x<0时,y<0.
点评 考查了二次函数的性质,抛物线的顶点式适合与确定抛物线的开口方向,顶点坐标,对称轴,最大(小)值,增减性等;抛物线的交点式适合于确定函数值y>0,y=0,y<0.

练习册系列答案
相关题目
7.(-5)2的平方根是( )
| A. | $\sqrt{5}$ | B. | 5 | C. | -5 | D. | ±5 |