题目内容
14.如果关于x,y的二元一次方程组$\left\{\begin{array}{l}5x+3y=31\\ x+y=p\end{array}\right.$的解是正整数,求整数p的值.分析 先求出方程组的解,根据方程组的解是正整数得到不等式组,求出p的取值范围,即可解答.
解答 解:二元一次方程组$\left\{\begin{array}{l}5x+3y=31\\ x+y=p\end{array}\right.$的解为$\left\{\begin{array}{l}x=\frac{31-3p}{2}\\ y=\frac{5p-31}{2}\end{array}\right.$
∵方程组的解是正整数,
∴$\left\{\begin{array}{l}{\frac{31-3p}{2}>0}\\{\frac{5p-31}{2}>0}\end{array}\right.$
解得:$\frac{31}{5}$<p<$\frac{31}{3}$,
∵p为整数,方程组的解为正整数,
∴p=7,9.
点评 本题考查了二元一次方程组的解,解决本题的关键是求出二元一次方程组的解.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
9.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AC=BD | C. | AB=BC | D. | AC⊥BD |
19. 如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
 如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )
如图所示,直线a∥b,∠B=16°,∠C=50°,则∠A的度数为( )| A. | 24° | B. | 26° | C. | 34° | D. | 36° |
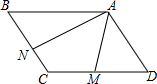 如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$.
如图,在?ABCD中,点M,N分别是边CD、BC的中点,AM=2,AN=4,且∠MAN=60°,则AB的长是$\frac{4\sqrt{13}}{3}$. 如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.
如图,在△ABC中,AB=AC,DE垂直平分AB交AC于点E,已知△BCE的周长为8,且AC-BC=2,求AB,BC的长.